Fourier 変換 f x L f x( ) ( ) ミラー指数(23) 逆格子点(23) d G 六方格子 hex X D L S D L S D S L 記号:対称性の高い点 表面上の点:ローマ字 内部の点:ギリシャ文字 いずれも大文字 613六方晶系の面指数 を用いる (h k l) # (h k j l) A B D O OAB = OAD OBD h k j = 0 利点:面の対称性が明らかになる この2つの面が等価であることがわかる · 六方晶の面を表す時にミラー指数でお馴染みの(hklm)について どうもh k = iという関係が成り立つみたいです。 ミラー指数については分かるのですが、何故この式が成り立つのか

Woa1 非水電解質二次電池用正極活物質とその製造方法 および 非水電解質二次電池 Google Patents
六方晶 ミラー指数 変換
六方晶 ミラー指数 変換-ここでは、六方晶を例にとってCohenの方法について述べる。六方晶におけるBlagg角 と格子定数およびMiller指数の関係は上に示した通りである。 いま、 λ2 3a2 = A (5) λ2 4c2 = B (6) h2 hk k2 = x (7) l2 = y (8) sin2 θ = z (9) とすれば、 z = Ax+By (10) となる。問下図のレンガ(辺の長さが異なる直方体)について、属する晶 系、点群、対称要素の種類と場所を示せ。 演習 問a≠b≠c, α≠β≠90º或は1º、γ=90ºなる関係を持つ系は 二斜晶系(diclinic)の定義に一致する。これは8番目の晶系とな るか。 単位胞の選び方




Wo14 号 窒化物半導体発光装置 Astamuse
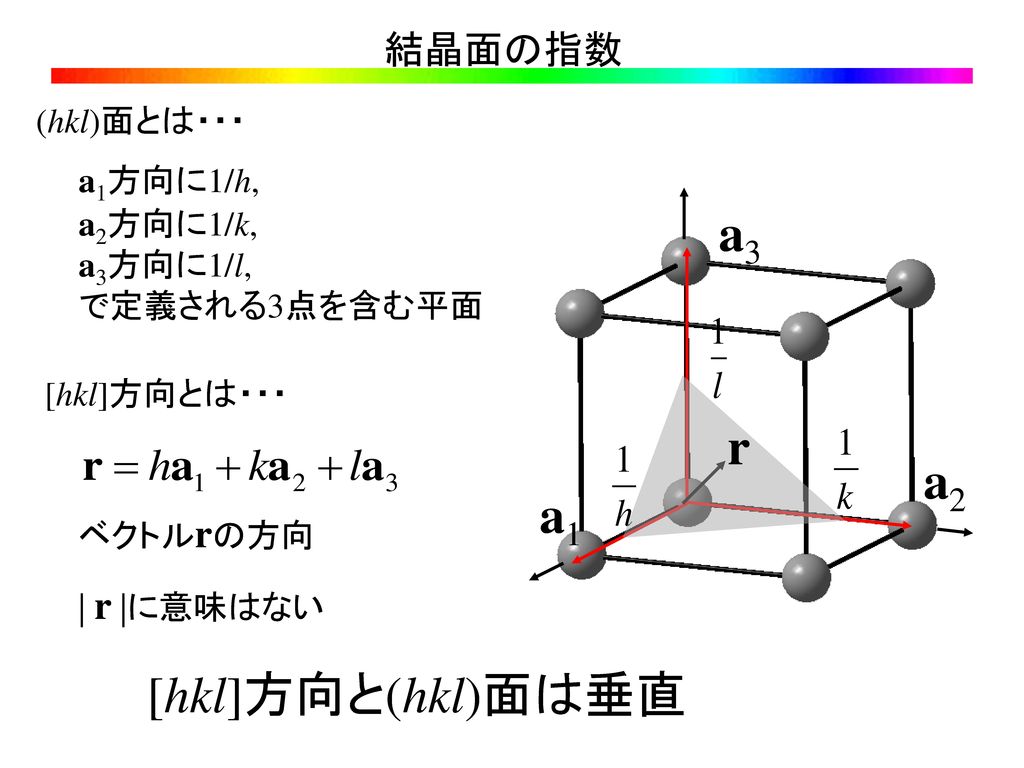
最密六方格子では,すべ り方向が底面内の 方向のみ. c軸を板厚方向にそろえ ると,板厚を減少させる ような2軸応力条件にお いて強度が向上. c軸に垂直な方向の引張 (あるいは圧縮)変形が 困難. = 集合組織硬化 Slip direction Biaxial tensile stressで切る平面のことである(ミラー指数のこと)。 (hkl)面とそれに垂直な逆格 子ベクトル K hkl 前ページの図に示すように、 逆格子ベクトル K hkl は(h k l) 面に垂直 であること意味している。 (証明) (h k l) 面上の以下の2本のベク をベクトルを考える。 a332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.
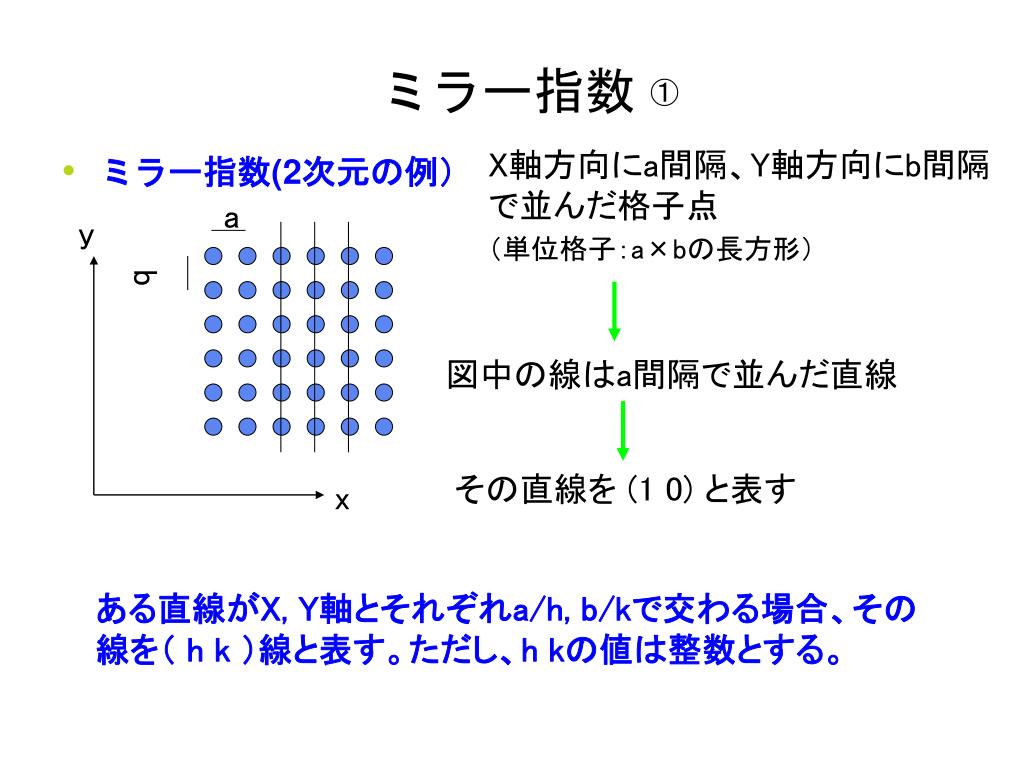
(7)複合六方格子のラウエ群は3か3mlで あり,31mで はあり得ない (8)複合六方格子は軸の取り方をまちがえると見かけ上, 単斜のC底心 になる (9)ピ ークサーチで格子定数を求める場合,指 数付けが うまくいけば,ピ ークデータ は10で よいミラー指数(Miller index) たまに、(0001)みたいに4桁のものを見掛けますよね。あれはhcp(六方最密格子)です。 基本ベクトルの長さは格子の境界を1とします) 上述した方法と全く同じに(a1 a2 a3 c)で、六方晶の面を表します。5 ・2格子面の同定 (a)ミラー指数 任意の面の表し方 (1)面と各軸との交点座標(x,y,z)を求める. (2)座標(x,y,z)を各格子定数で割った逆数(h,k,l)を求める. (3)座標成分を最小整数比に直し,括弧にくくって表す.
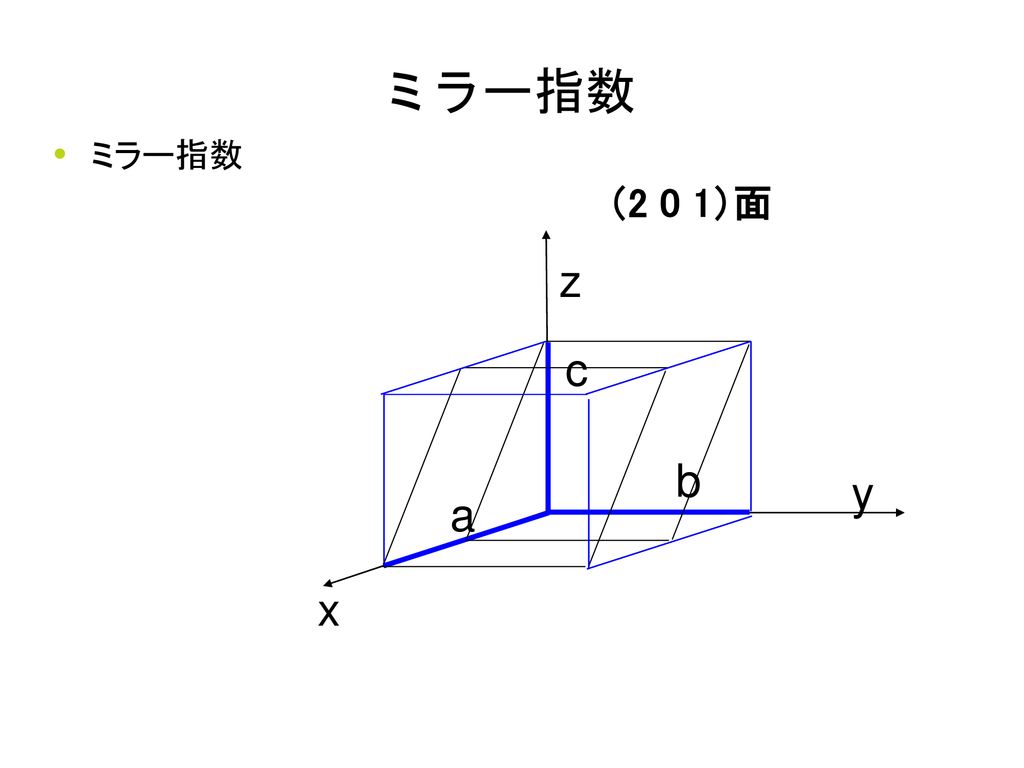
指数(ミラー(Miller) 指数)と呼ぶ。図の例では、A = 3, B = 2, C = 2 であるので、 1 3 2 2 であり、従ってミラー指 数は(2 3 3) となる。指数の0 は切片が無限大であること、つ まり切片を持たないことを意味する。 (100) (010) (011) (111) 図4 格子面(ミラー指数)の例EditLattice planes を選ぶと表示されるウインドウ(図37(a))で面指数を入力します。表示 面の原点からの距離も入力できここでは05 としてありますので原点とunit cell の中間に 表示されます。さらに、格子面と等価な面も指定して(図(b))、格子面で囲まれた6 角柱7ミラー指数 8逆格子 9回折条件 結晶構造解析i 結晶構造解析ii 結晶欠陥(転位,空孔,格子間挿入,置換) 結晶成長 立方格子 面心格子,六方格子 ブリルアンゾーン 空間群 光学モードと音響モード フォノン=場の量子化もどき ボゴリューボフ変換 2次元格子




Images Of 六方晶 Japaneseclass Jp




ミラー指数 Monozukuri Hitozukuri 日本のものづくり
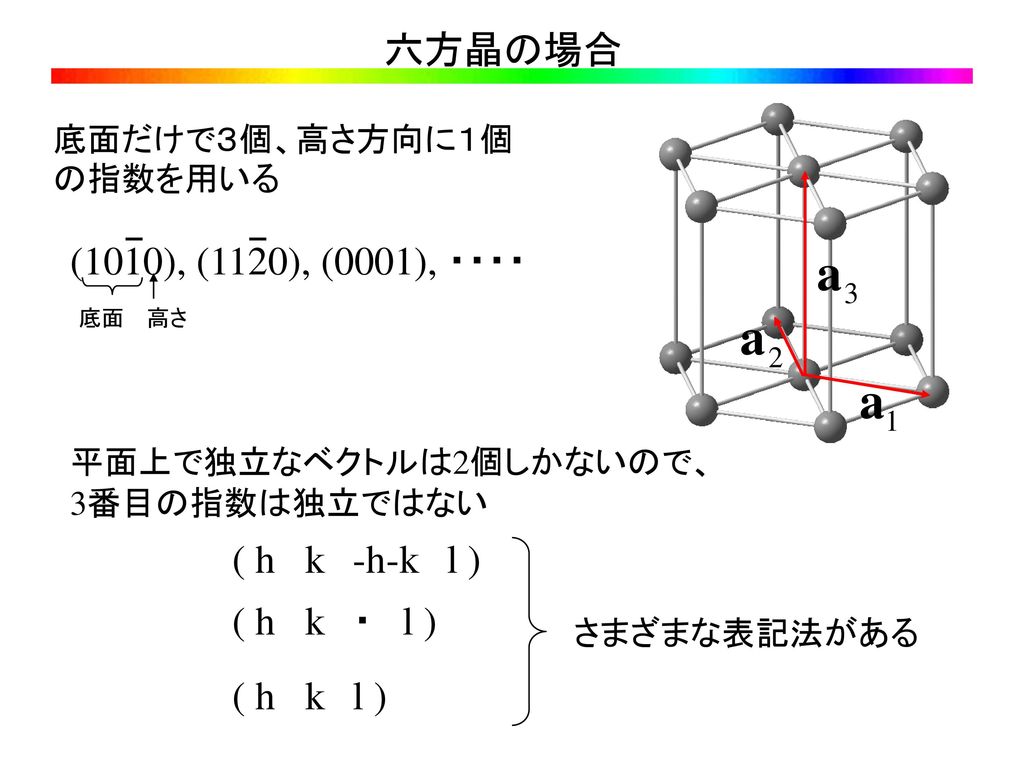
六方晶 hexagonal 菱面体晶 rhombohedral 直方晶 orthorhombic 単斜晶 monoclinic 三斜晶 triclinic 図123 ブラベー格子 32.結晶構造!ミラー指数(ミラーしすう)は結晶の格子中における結晶面や方向を記述するための指数である 。 英国の鉱物学者ウィリアム・ハロウズ・ミラー (William Hallowes Miller) によって考案された。 ミラー指数には、面指数と方向指数(方位指数)の2種類がある。面指数は結晶や格子をどのような平面で六方晶の場合 a 1 a 2 a 3 底面だけで3個、高さ方向に1個 の指数を用いる (1010), (11), (0001), ・・・・ 底面 高さ 平面上で独立なベクトルは2個しかないので、 3番目の指数は独立ではない ( hkhkl ) ( hk・l ) ( hkl ) さまざまな表記法がある




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



半導体物理 結晶構造について 2 Sciencompass
ミラー指数 463 ミラー指数の表記 < 100 > = 100,010, 001 {111} = (111),(1 11),(1 1 1),(111 ) 方向: 面:A = b = c,α=β=γ=90° ⇨立方晶 a ≠b = c,α=β=γ=90° ⇨正方晶 単位格子:3つの長さ(a, b, c) と3つの角度(α,β,γ)で規定される 原点 a ≠b≠c,α=β=γ=90° ⇨斜方晶 a b c x,y,z座標軸を描く ときは六方晶,非対称極点図ODF解析の注意点 2.3 指数<->4指数変換 3.3指数<->4指数変換とX軸の関係をHexaConvertソフトウエアで確認 4.LaboTexとTexToolsで対称極点図を非対称ODF解析




2 ミラー指数についてpart2 Youtube



モデラ Advance Nanolabo ドキュメント
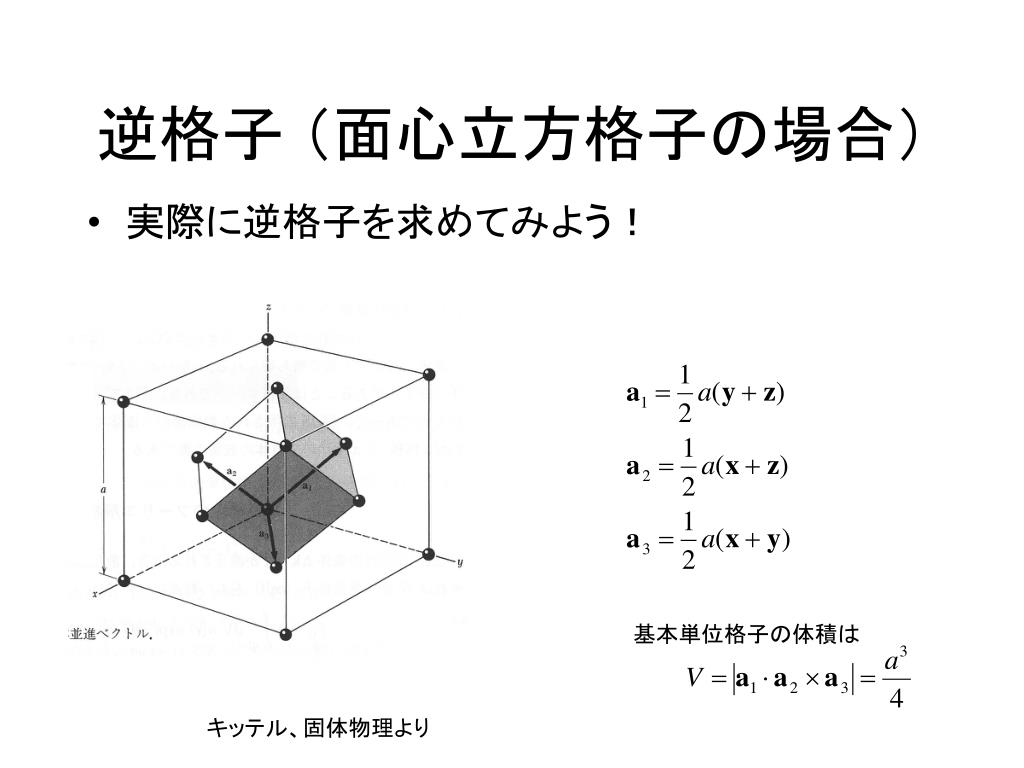
· この面と原点の距離が (hkl) 面の 面間隔d_ {hkl} に等しく d_ {hkl}=\frac {a} {\sqrt {h^2k^2l^2}} で与えられる。 (hkl) 面の面間隔 d_ {hkl} と、ミラー指数を n 倍した (nh~nk~nl) 面の面間隔 d_ {nhkl} には次の関係が成り立つ。 \begin {align*} d_ {nhkl}&=\frac {a} {\sqrt { (nh)^2 (nk)^2 (nl)^2}} \\ &=\frac {a} {n\sqrt {h^2k^2l^2}} \\ &=\frac {d_ {hkl}} {n} \end {align*}150 日本結晶学会誌 第59巻 第4号(17) 日本結晶学会誌 59,(17) 対称性と群論() ミラー指数,ラウエ指数と消滅則 ロレーヌ大学結晶学教室 ネスポロ マッシモ Massimo NESPOLO Miller Indices, Laue Indices量子化学計算ソフト(りょうしかがくけいさんソフト)は量子化学的手法を実装したソフトウェアのこと。 計算化学の分野において利用される。 その他の六方晶の場合は、1つのデータではaとcを求めることはできません。 いくつかのピーク角度と面



モデラ Advance Nanolabo ドキュメント




Wo07 号 単結晶サファイア基板 Astamuse
ミラー指数 ミラー指数の表記 < 100>=100,010,001 { 111}=(111),(1 11),(11 1),(111) 方向: 面:19 結晶面の指数 三次元格子の面に対するミラー指数は(h k l)で 与えられる。 1) 格子定数 a 1, a 2, a 3 を単位として面が結晶軸 2 を切り取る長さを表す。 2) これらの数の逆数を求め、じ比を なす3個の最小の整数に簡約する。 これをその結晶面の面指数(h k l)とする。 aミラー指数(ミラーしすう)は結晶の格子中における結晶面や方向を記述するための指数である 。 英国の鉱物学者ウィリアム・ハロウズ・ミラー (William Hallowes Miller) によって考案された。 ミラー指数には、面指数と方向指数(方位指数)の2種類がある。面指数は結晶や格子をどのような平面で




Woa1 化合物エピタキシャル層の製造方法 化合物エピタキシャル層 半導体積層構造および半導体発光デバイス Google Patents




Wo14 号 半導体発光装置 Astamuse
ミラー指数 u,v,w 格子点座標 uvw:原点と格子点を結んだ方向を示す指数 <uvw>:同型の晶帯軸の指数 (hkl) :結晶面の指数 hkl :逆格子の座標、または反射X線の指数 {hkl} :同型の面の指数 6 · ミラー指数 ミラー指数の概要 ナビゲーションに移動検索に移動 立方晶結晶での異なるミラー指数をもつ面 方向指数の例 x,y,z軸との切片からミラー指数を決定する例。左は(111)、右は(221)ミラー指数には,面指数と方向指数(方 · 六方結晶の場合は(0001)というような表し方ですね。 いわゆるc軸が4桁目になります。(h,k,l,m)の場合、h k = l の関係があります。 参考URLに出典例を書きましたが、"ミラー指数" "0001"で検索すると、関連ページが56件ありました。



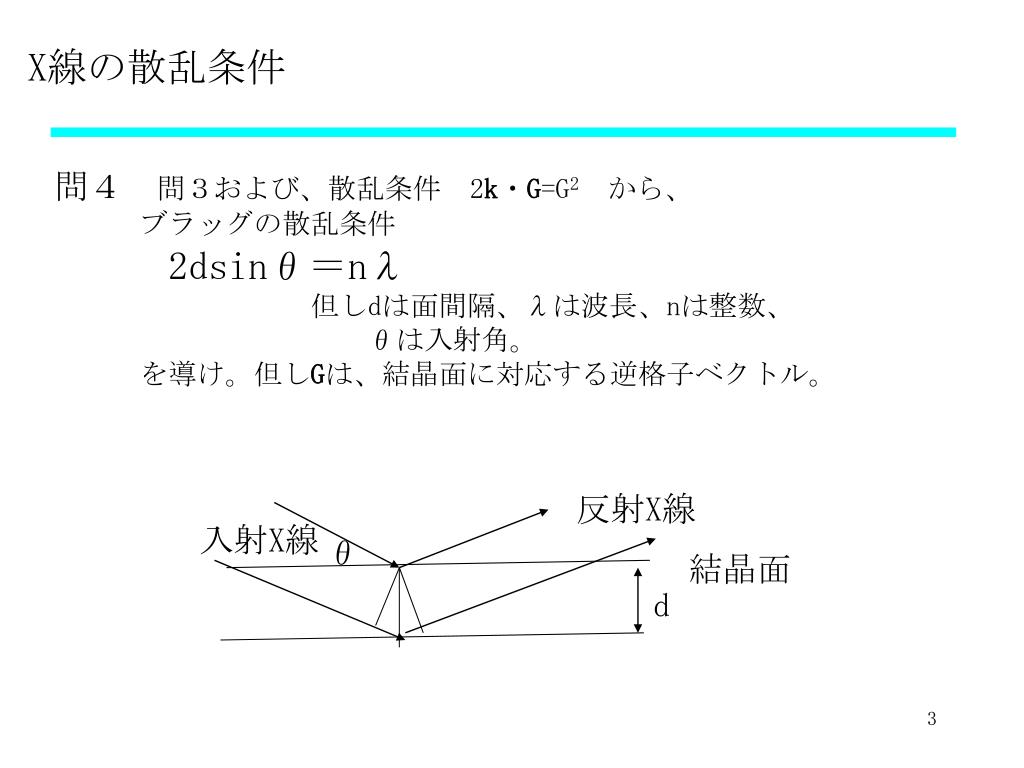
x線結晶解析におけるラウエの条件式とブラッグの条件式




逆 格子 ベクトル
Title PowerPoint プレゼンテーション Author Yoichi Nabetani Last modified by nabetani Created Date 12/28/04 AM Document presentation format · 六方晶4指数表示の高次元解釈― @aki_kuwa 氏による解説 @aki_kuwa 氏に六方晶を4指数で表示する意義について、高次元の観点で大変わかり易く解説していただきました。 高次元から4指数を見ると大変見通しがよく、広く知られるべきと思います。 より詳細にという計算で得られる。 反射指数 hkl と面間隔 d, 回折角 2θ のリストを作成する 実験で測定できる回折角 2θ の範囲は有限に限られているから,格子定数から「測定範囲 内に出現しうるすべての反射指数 hklと面間隔値 d,回折ピークの位置 2θ のリスト」を生 成できれば,文献に記載されて




13 0631号 sicエピタキシャルウエハおよびそれを用いたsic半導体素子 Astamuse




逆 格子 ベクトル
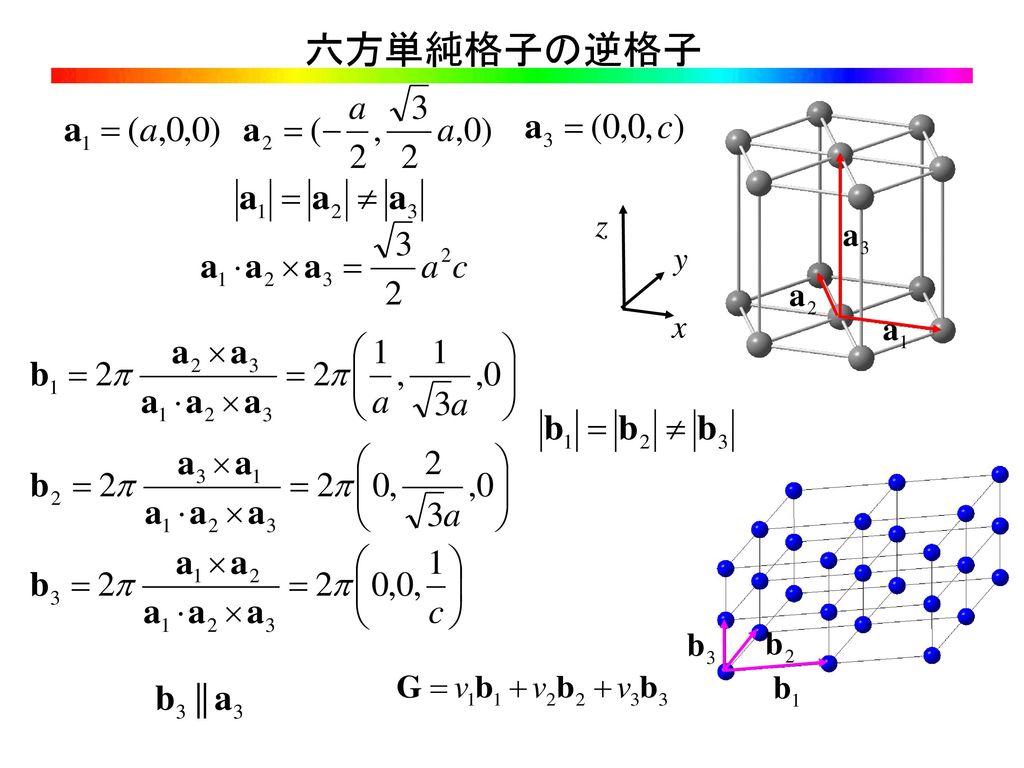
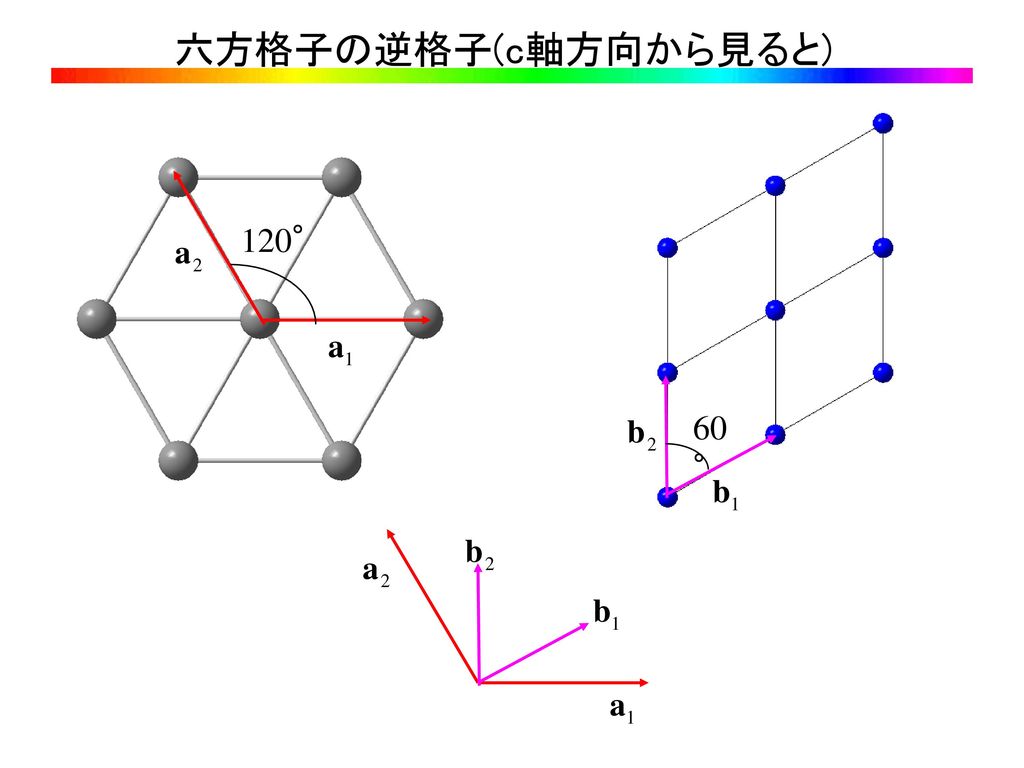
最密六方格子(hexagonal closepacked lattice)の原子配置 軸比(axial ratio) c/aの値.理想的な場合(各原子が球形と見な せる場合)には,軸比が となる.1633= 8/3 単位格子 22六方晶系の面指数 a b d a b c a b d c, , , , , o を用いる (h k l) → (h k j l) A B D a h a k O a j OAB = OAD OBD 1 1 1 sin1 sin60 sin60 2 2 2 a a a a a a h k h j j k q q q h k j = 0 利点:面の対称性が明らかになる (1 2 1) (1 1 1) (1 2 1 1) (1 1 2 1) この2つの面が等価であることがわかるまず、結晶の対称性を数式的に扱うために直交座標の回転による座標変換公式を導く。 旧直角座標系におけるベクトルpの成分を(, とし、変換後の新座標系におけるベク トルp' の成分を(, と置く。また両座標系の原点は一致させるものとする。この両
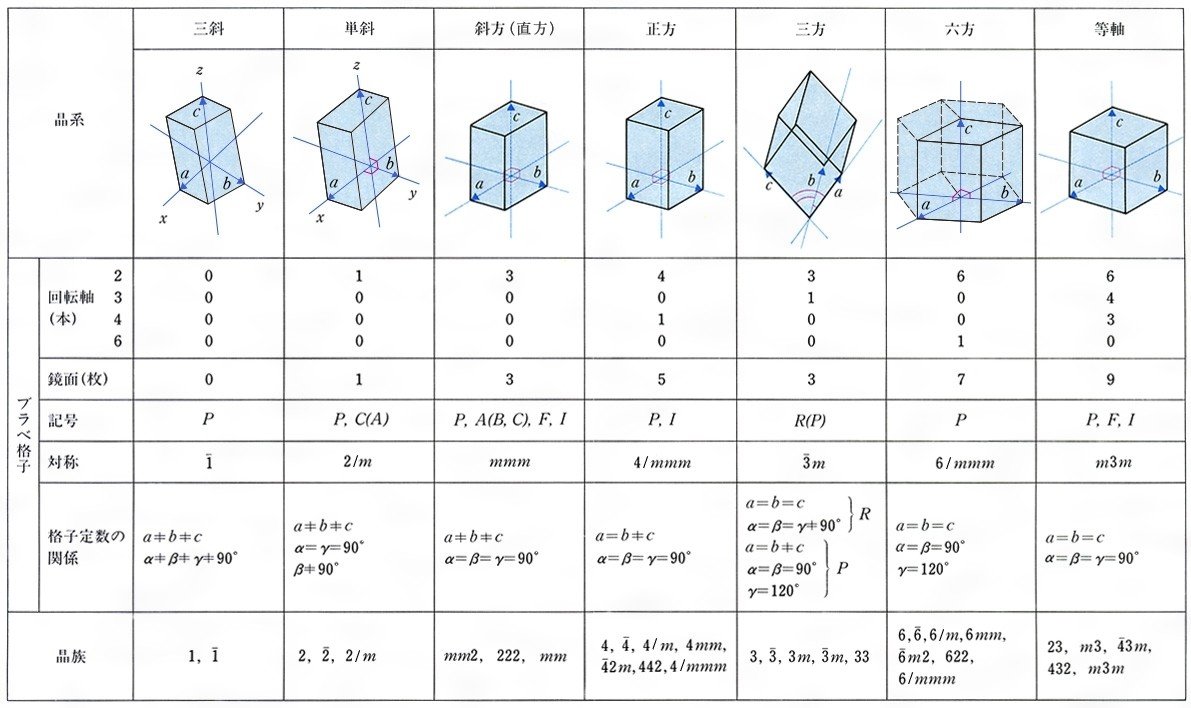



Images Of 晶系 Japaneseclass Jp




2 2 1 ブラベー格子 単位格子 原子が配列している周期的な配列の中で最も 単純で最小な単位 Ppt Download
六方晶 六方晶においては慣用的に下図のような a 1 , a 2 , a 3 , c の四つの軸を用いて方向面を表し,指数を( hklm )と書きます。この方法では,Z軸方向の指数は0001となります。この4軸を用いると,a 1 , a 2 , a 3 方向を現す指数 hkl の間には, h k = lエネルギー・ 1 Ry = eV ・ 1 eV = kJ/mol = e19 J = cm1 ・ 1 cal = 4184 J ・ 1 cm1 = E4 eV 長さ ・ 1 au(bohr) = A 超越数 ・ e = ・ pi = 物理定数 ・ k = e23 J/K = e6 eV/K (Boltzmann const) ・ N = e23 /mol (Avogadro const) ・ R = 1451 J/molK (Gas const) ・ e =結晶構造ギャラリー 本結晶構造ギャラリーの結晶構造図は、もともと、02年8月2日(金)の「産業技術総合研究所 関西センター 一般公開」で公開したものです。



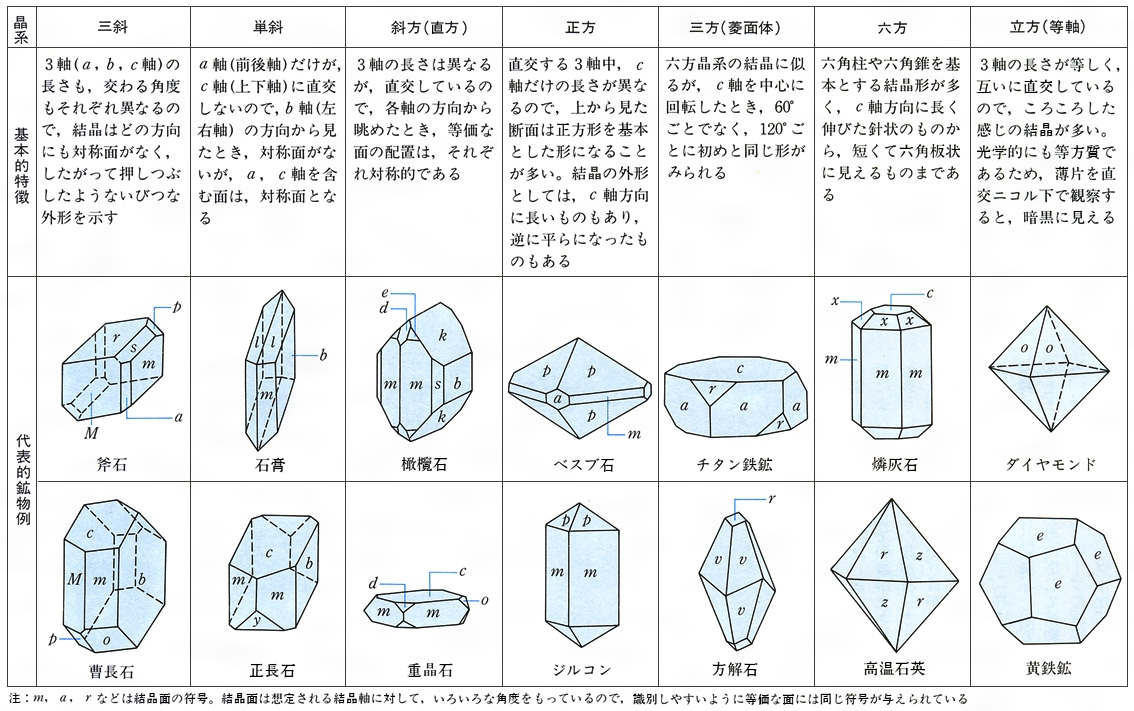
鉱物の結晶




ミラー指数 Wikiwand
図は六方晶を示したものである。 ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で · 六方晶 ミラー指数 について 今六方晶のミラー指数が 001 100 101 102 110 と表されております。 ここで、この3桁のミラー指数を全て4桁で表すとどのようになりますか? よろしくお願いしえ,高感度カメラによってコンピュータに取り込んだ後,Hough 変換によって結晶方位の指数付 けがなされる。SEMEBSD 法についてはStojakovic(12)などを参照のこと。 SEMEBSD 法による結晶方位の測定結果はオイラー角(φ 1, Φ, φ 2)という3 つの角度の組み合



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download




13 0631号 sicエピタキシャルウエハおよびそれを用いたsic半導体素子 Astamuse
知ることができる。散乱振幅F(q) は、数学的には電子密度ρ(x) のフーリエ変換になっている。 4六方最密構造のもととなるA 方式(p10)による3 段構造を真上から見たのが下図であり, 赤色剛球に注目すると,12 個の剛球が最近接しているのがわかる。 よって,六方最密構造の任意の剛球と最近接する剛球の数は12 である。



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



半導体物理 結晶構造について 2 Sciencompass




14 5615号 立方晶炭化珪素半導体基板及び立方晶炭化珪素層 Astamuse



半導体物理 結晶構造 3 ミラー指数 Sciencompass




前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download




Woa1 非水電解質二次電池用正極活物質とその製造方法 および 非水電解質二次電池 Google Patents




Wo14 号 窒化物半導体発光装置 Astamuse




Woa1 非水電解質二次電池用正極活物質とその製造方法 および 非水電解質二次電池 Google Patents



モデラ Advance Nanolabo ドキュメント




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download




Wo10 号 窒化物系半導体素子およびその製造方法 Astamuse



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




Wo11 号 窒化ガリウム系化合物半導体発光素子 Astamuse




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



x線結晶解析におけるラウエの条件式とブラッグの条件式



格子面間隔の計算方法 六方晶 Sciencompass




15 号 窒化物半導体構造およびそれを製造する方法 Astamuse



x線結晶解析におけるラウエの条件式とブラッグの条件式




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



Space Group For Crystal Structure Analysis



逆 格子 ベクトル 実格子と逆格子の対応 物理のかぎしっぽ



結晶とは コトバンク
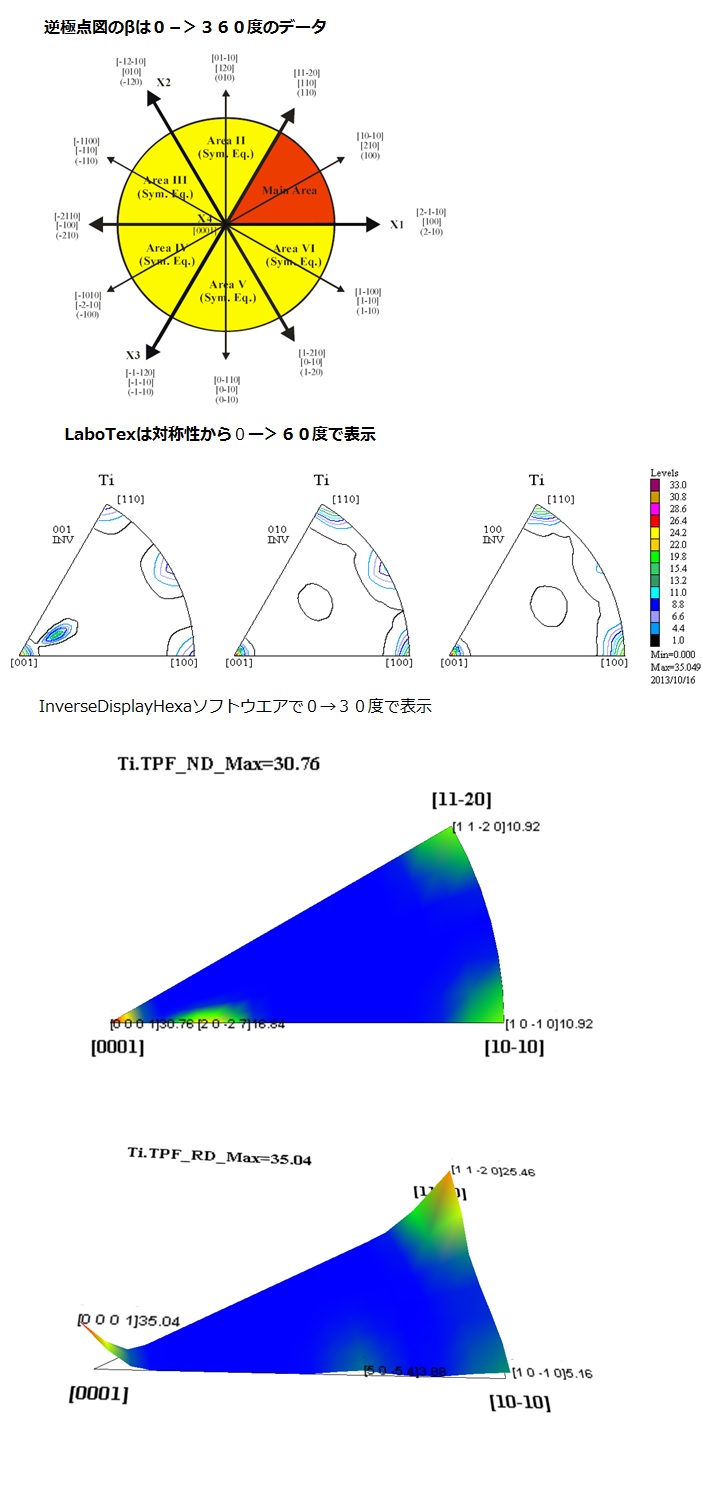



六方晶の逆極点図を表示するinversedisplayhexaソフトウエア 極点測定 解析 Odf Labotexの導入 helpertex




โน ตของ 専門 講義 結晶構造について ช น Clear
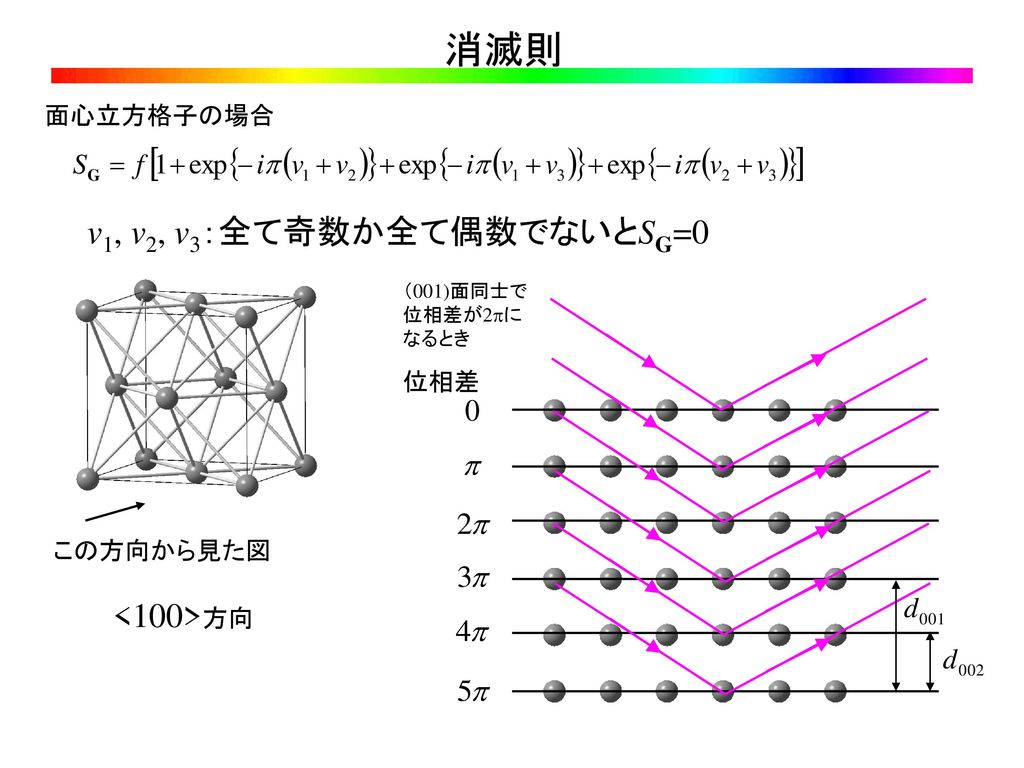



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
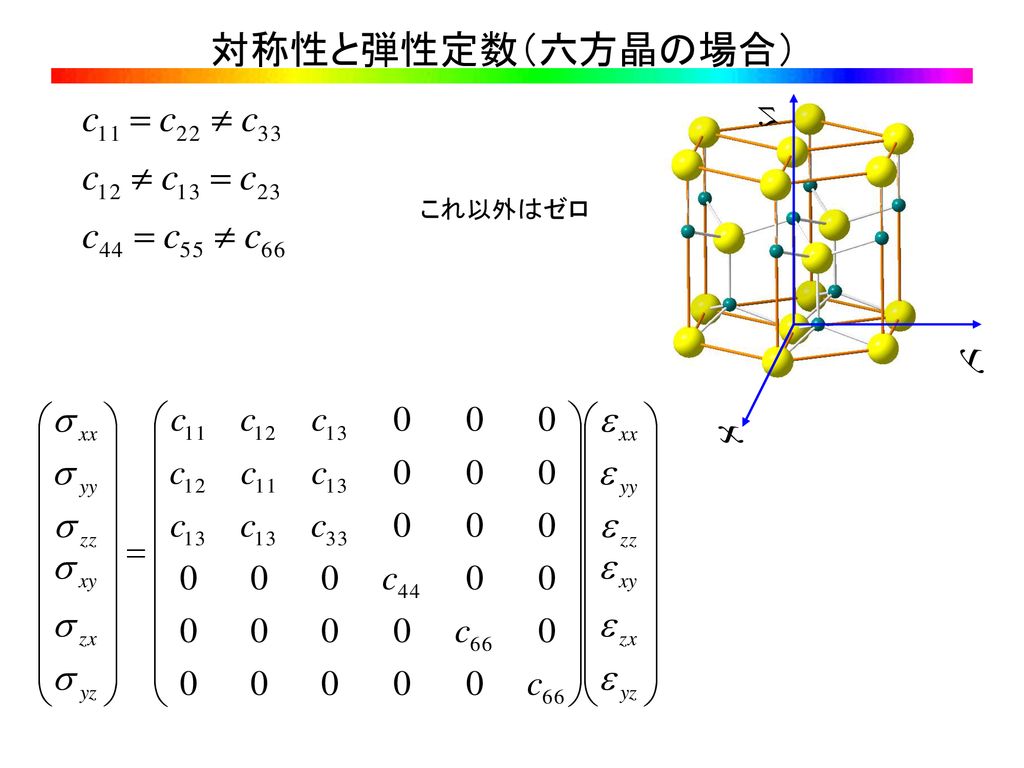



結晶工学特論 第2回目 前回の内容 半導体デバイス Led Ld Hemt 半導体デバイスと化合物半導体 種類の豊富さ 直接遷移型 Ppt Download




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



Information



逆 格子 ベクトル 実格子と逆格子の対応 物理のかぎしっぽ



Images Of 六方晶 Japaneseclass Jp




Woa1 リチウムイオン二次電池用正極活物質及びリチウムイオン二次電池 Google Patents
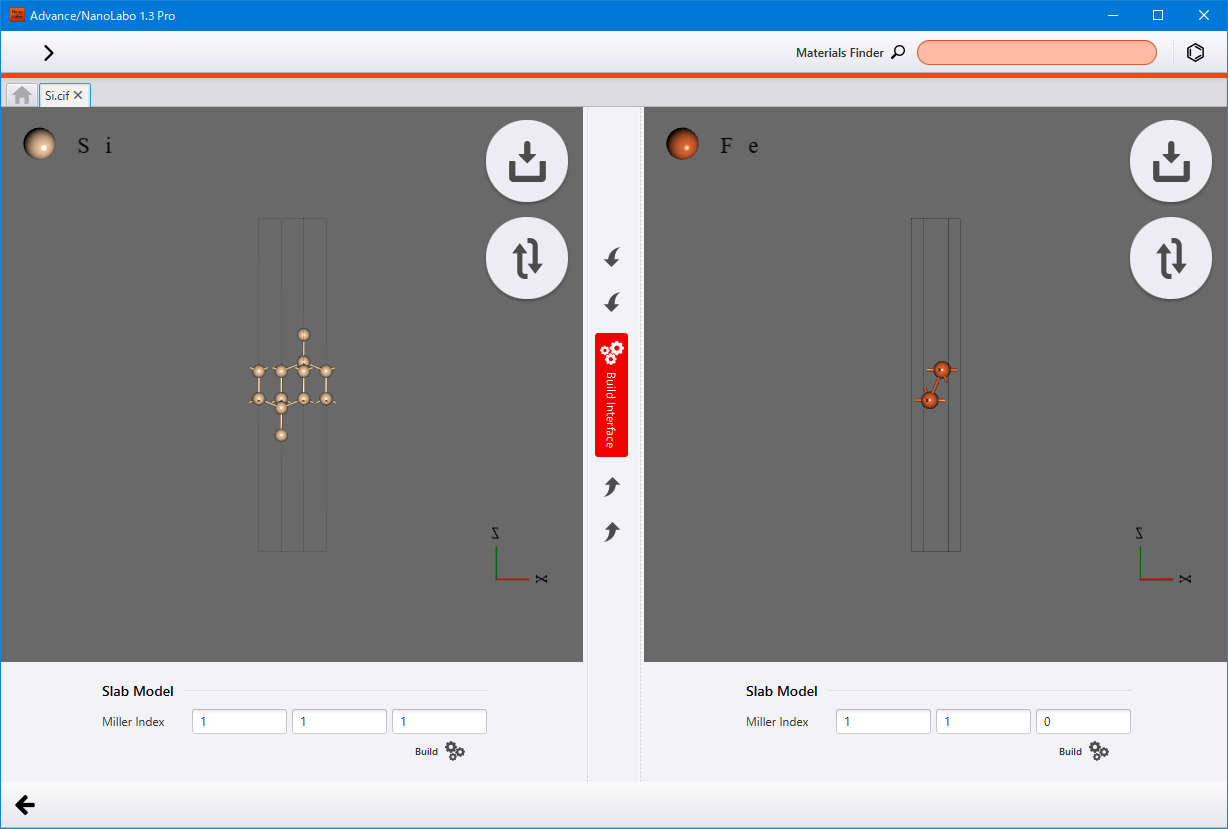



モデラ Advance Nanolabo ドキュメント



x線結晶解析におけるラウエの条件式とブラッグの条件式




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



x線結晶解析におけるラウエの条件式とブラッグの条件式



x線結晶解析におけるラウエの条件式とブラッグの条件式




ミラー指数 Wikipedia



0 件のコメント:
コメントを投稿